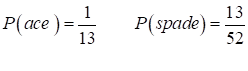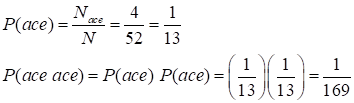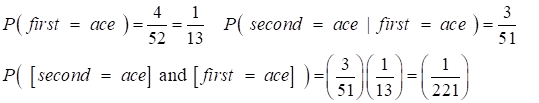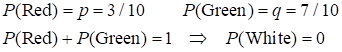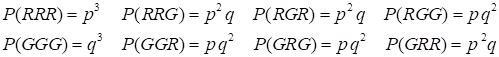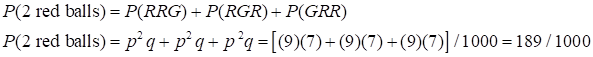|
ADVANCED SCHOOL MATHEMATICS PROBABILITY Ian Cooper email matlabvisualphysics@gmail.com |
|
This
section will give you a brief introduction to the theory and applications of
probability. Let
If A is certain to happen then If A is certain to not happen then Consider random
experiments such as coin tossing, throwing dice, drawing balls from an urn,
lotteries, dealing cards in which the outcome of events are all equally likely outcomes. For example, if an experiment has N possible outcomes, all
equally likely and Ns
of these
leads to success, then, the probability of success is Probability of
success Example What is the probability of drawing an ace from a shuffled pack of
cards?
The event that A does not occur is written as
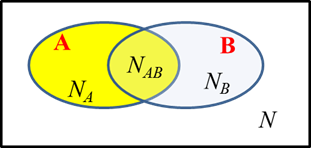
COMBINING PROBABILITIES Consider
an experiment with N equally likely outcomes, involving two events A and B.
However, before deciding how to combine probabilities it is necessary to know
whether the two events A
and B are mutually exclusive (A and
B cant
happen together) or not mutually
exclusive. MUTUALLY EXCLUSIVE
EVENTS
Probability of A
Probability of B
Probability that of either
event A or event B
occurs is
the sum
of the probability of A
and B Example What is the probability of drawing an ace or a king from a
shuffled pack of cards?
For n mutually exclusive
outcomes NON MUTUALLY EXCLUSIVE
EVENTS
Two events may occur
together, for example, drawing an ace or a spade from a pack of card. When two events are not mutually exclusive Example What is the
probability of drawing an ace or a spade from a shuffled pack of cards?
Alternatively use
the original definition of probability MULTIPLYING PROBABILITIES The probability of
both A and
B occurring
is called the joint probability of A and
B or
the product of A
and B. provided
A is
not affected by the outcome of B
and B is not affected by
the outcome of A,
i.e. A and
B must independent. Example A card is drawn from two shuffled packs of cards. What is the
probability that two aces are drawn? Example A number is
selected from the set {1 2 3 4 5 6 7 8 9}. Event A occurs if the number is even and event B occurs if the
number is less than 6. N = 9 Event
A: even number {2 4 6 8}
Event B: < 6
{1 2
3 4
5} Events A and
B are
not mutually exclusive since {2 4} occur in both events. What is the
probability that events A and B both occur? A and
B {2 or 4}
What is the
probability that events A or B both occur? A or
B Alternatively NON-INDEPENDENT EVENTS A card is draw from
a single pack, then a second card is drawn without
putting the first card back in the pack. What is the probability that I
draw two aces? Hence, the probability
of both cards being aces is
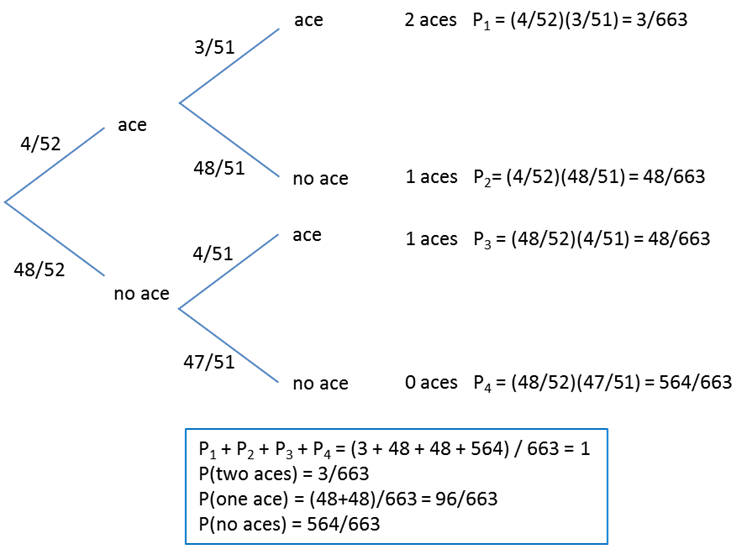
TREE DIAGRAMS Tree
diagrams are very useful to trace possible outcomes of two or more stages of
an experiment and then to calculate the probabilities of certain final
events. Tree diagram for drawing two cards from a pack of card
probabilities of aces being drawn
What is the probability of ace being drawn as the second card
when the first card was not an ace ? Example A large number of
red and green balls are in an urn in the ratio of red to green of 3 to 7. A
ball is selected and then returned, then another ball is selected and the
process is repeated again. Find the probability for 3 balls being chosen such
that (1) exactly two are red; (2) at least one is green; (3) three are all
red or three are all green; and (4) one ball is white. You can draw a tree
diagram to work out all the combination of events. On each selection of a
ball there are two possible outcomes R or G, therefore, the total number of
outcomes for the drawing of the three balls is (1) (2) (3) (4) There are no white balls Notations Intersection AND Union OR Example A pair of dice is
thrown. What is the probability that they show a total of 3?
Example A card is drawn
randomly from a pack of 52 cards. What is the probability that is an
odd-numbered card?
|